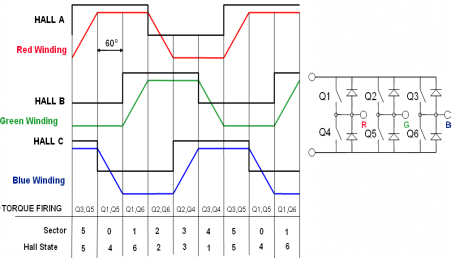PID Closed Loop Controls

Electric Motor Controls - PID

Industrial/Aerospace/Military Specifications

Designs by the inventor of the Slotless Wide Airgap Motor

Control/Drive Hardware

The figure shows a typical 3-phase closed loop motor driver circuit configuration. Feedback can be accomplished by various means, such as resolvers, optical encoders, synchros and Hall devices. There are many MCUs available for Electronically Commutated (EC) Motors.

The method of control is usually determined by the application and the shape of the motor back-emf. The permanent magnet synchronous motor (PMSM) is a close relative of the brushless DC (BLDC) motor. Both motors have a permanent magnet rotor and windings on the stator. The principle difference between these two motors is the kind of drive signals that are supplied to the motor by the inverter. There are a variety of control schemes available among which the Six-Step and Sine Wave controls are the most common. Many of them can be used on the same motor and control/drive circuit just by changing the program on the microcontroller (MCU).

Six Step

The six-step waveform control was historically the first method for controlling brushless machines, because it was simple and was easy to impliment using discreet logic chips. There were no MCUs available at that time. This method is still in common use.

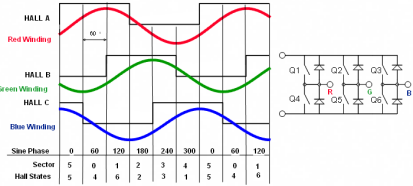Sine Wave

The MCU or digital signal processor made the sine wave controls feasible. There are a variety of algorithms available to create sine wave drives using the identical hardware as the six-step method. This method is most favourable where the back-emf is also a sine wave.

PID

A proportional–integral–derivative controller (PID controller) is a generic control loop feedback mechanism (controller) widely used in industrial control systems – a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error by adjusting the process control inputs. In the absence of knowledge of the underlying process, PID controllers are the best controllers. However, for best performance, the PID parameters used in the calculation must be tuned according to the nature of the system – while the design is generic, the parameters depend on the specific system.

Proportional Term

The proportional term (sometimes called gain) makes a change to the output that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant Kp, called the proportional gain.

A high proportional gain results in a large change in the output for a given change in the error. If the proportional gain is too high, the system can become unstable (see the section on loop tuning). In contrast, a small gain results in a small output response to a large input error, and a less responsive (or sensitive) controller. If the proportional gain is too low, the control action may be too small when responding to system disturbances.

Integral Term

The contribution from the integral term (sometimes called reset) is proportional to both the magnitude of the error and the duration of the error. Summing the instantaneous error over time (integrating the error) gives the accumulated offset that should have been corrected previously. The accumulated error is then multiplied by the integral gain and added to the controller output. The magnitude of the contribution of the integral term to the overall control action is determined by the integral gain.

The integral term (when added to the proportional term) accelerates the movement of the process towards setpoint and eliminates the residual steady-state error that occurs with a proportional only controller. However, since the integral term is responding to accumulated errors from the past, it can cause the present value to overshoot the setpoint value (cross over the setpoint and then create a deviation in the other direction). For further notes regarding integral gain tuning and controller stability, see the section on loop tuning.

Derivative Term

The rate of change of the process error is calculated by determining the slope of the error over time (i.e., its first derivative with respect to time) and multiplying this rate of change by the derivative gain Kd. The magnitude of the contribution of the derivative term (sometimes called rate) to the overall control action is termed the derivative gain, Kd.

The derivative term slows the rate of change of the controller output and this effect is most noticeable close to the controller setpoint. Hence, derivative control is used to reduce the magnitude of the overshoot produced by the integral component and improve the combined controller-process stability. However, differentiation of a signal amplifies noise and thus this term in the controller is highly sensitive to noise in the error term, and can cause a process to become unstable if the noise and the derivative gain are sufficiently large. Hence an approximation to a differentiator with a limited bandwidth is more commonly used. Such a circuit is known as a Phase-Lead compensator.